ent
BLUF:-
A subtle mistake(?) that means ent requires nuanced usage. The program seems to be a mix of randomness test and entropy measurement. But those are incompatible. Use it carefully either with the -c option for IID min.entropy measurement (if you have IID data), or as a compact randomness test focusing on bit/byte distribution only.
ent is:-
“a program, ent, which applies various tests to sequences of bytes stored in files and reports the results of those tests. The program is useful for evaluating pseudorandom number generators for encryption…”
In “evaluating pseudorandom number generators for encryption”, the required entropy rate is 1 bit/bit or 8 bits/byte. Anything substantially less is useless for cryptography. There is no need to measure it as the only result concerning us is a pass/fail determination within agreed confidence bounds, à la the other standard randomness tests like dieharder. Yet there are no bounds and no determination of any p values for confidence other than for a bit/byte $ \chi^2 $ distribution.
And it can’t be used for general entropy measurement in it’s default setting, as it reports the wrong type of entropy. Cryptography focuses on the most conservative min.entropy $(H_{\infty})$, not Shannon entropy. ent reports Shannon entropy which is always higher for all sample distributions other than uniform. See Note 1. And uniform distributions are uncommon from most entropy sources.
As an example, see the following entropy calculations for our Zenerglass compared with ent:-
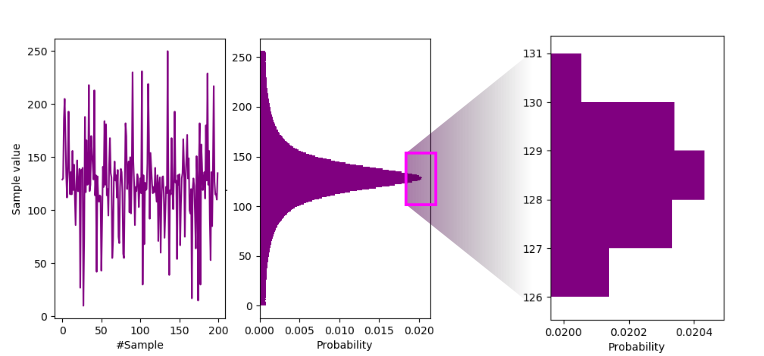
Sample waveform and histogram.
$ ent /tmp/raw-zenerglass.bin
Entropy = 7.125868 bits per byte.
Optimum compression would reduce the size
of this 10025000 byte file by 10 percent.
Chi square distribution for 10025000 samples is 16920202.99, and randomly
would exceed this value less than 0.01 percent of the times.
Arithmetic mean value of data bytes is 127.8980 (127.5 = random).
Monte Carlo value for Pi is 3.767184392 (error 19.91 percent).
Serial correlation coefficient is 0.000042 (totally uncorrelated = 0.0).And now the same with the -c argument:-
$ ent -c /tmp/raw-zenerglass.bin
Value Char Occurrences Fraction
0 7629 0.000761
1 7653 0.000763
2 7703 0.000768
3 7667 0.000765
4 7585 0.000757
5 7541 0.000752
6 7738 0.000772
7 7530 0.000751
8 7649 0.000763
9 7916 0.000790
10 7815 0.000780
11 7888 0.000787
12 7812 0.000779
13 7722 0.000770
14 7836 0.000782
15 7884 0.000786
16 7769 0.000775
17 8026 0.000801
18 8076 0.000806
19 8114 0.000809
20 8188 0.000817
21 8269 0.000825
22 8295 0.000827
23 8445 0.000842
24 8322 0.000830
25 8484 0.000846
26 8568 0.000855
27 8554 0.000853
28 8599 0.000858
29 8657 0.000864
30 8689 0.000867
31 8927 0.000890
32 9114 0.000909
33 ! 8956 0.000893
34 " 9438 0.000941
35 # 9417 0.000939
36 $ 9400 0.000938
37 % 9494 0.000947
38 & 9717 0.000969
39 ' 9818 0.000979
40 ( 9978 0.000995
41 ) 10253 0.001023
42 * 10225 0.001020
43 + 10372 0.001035
44 , 10512 0.001049
45 - 10827 0.001080
46 . 10878 0.001085
47 / 11050 0.001102
48 0 11279 0.001125
49 1 11469 0.001144
50 2 11779 0.001175
51 3 11992 0.001196
52 4 12154 0.001212
53 5 12136 0.001211
54 6 12436 0.001240
55 7 12819 0.001279
56 8 12959 0.001293
57 9 13087 0.001305
58 : 13561 0.001353
59 ; 13771 0.001374
60 < 13962 0.001393
61 = 14319 0.001428
62 > 14674 0.001464
63 ? 14984 0.001495
64 @ 15101 0.001506
65 A 15492 0.001545
66 B 15708 0.001567
67 C 16220 0.001618
68 D 16881 0.001684
69 E 16773 0.001673
70 F 17482 0.001744
71 G 17902 0.001786
72 H 18603 0.001856
73 I 18580 0.001853
74 J 19480 0.001943
75 K 19861 0.001981
76 L 20273 0.002022
77 M 20877 0.002082
78 N 21682 0.002163
79 O 22225 0.002217
80 P 22818 0.002276
81 Q 23498 0.002344
82 R 23911 0.002385
83 S 25155 0.002509
84 T 25932 0.002587
85 U 26688 0.002662
86 V 27833 0.002776
87 W 28910 0.002884
88 X 29731 0.002966
89 Y 30790 0.003071
90 Z 32110 0.003203
91 [ 33375 0.003329
92 \ 34927 0.003484
93 ] 35920 0.003583
94 ^ 37567 0.003747
95 _ 39099 0.003900
96 \` 40634 0.004053
97 a 42311 0.004221
98 b 44602 0.004449
99 c 46932 0.004681
100 d 49694 0.004957
101 e 52101 0.005197
102 f 55506 0.005537
103 g 58534 0.005839
104 h 61869 0.006171
105 i 66057 0.006589
106 j 69233 0.006906
107 k 74557 0.007437
108 l 78570 0.007837
109 m 84024 0.008381
110 n 89237 0.008901
111 o 95117 0.009488
112 p 101310 0.010106
113 q 107555 0.010729
114 r 114364 0.011408
115 s 122401 0.012210
116 t 129663 0.012934
117 u 137579 0.013724
118 v 146432 0.014607
119 w 154338 0.015395
120 x 163134 0.016273
121 y 170492 0.017007
122 z 179140 0.017869
123 { 186401 0.018594
124 | 191994 0.019152
125 } 198691 0.019820
126 ~ 201911 0.020141
127 203852 0.020334
128 204840 0.020433 <==== Most common.
129 203921 0.020341
130 201048 0.020055
131 197565 0.019707
132 192290 0.019181
133 186358 0.018589
134 178818 0.017837
135 171112 0.017069
136 162263 0.016186
137 155183 0.015480
138 146806 0.014644
139 138832 0.013849
140 129806 0.012948
141 121692 0.012139
142 114243 0.011396
143 108013 0.010774
144 101033 0.010078
145 94650 0.009441
146 89661 0.008944
147 84122 0.008391
148 79370 0.007917
149 74085 0.007390
150 69755 0.006958
151 66155 0.006599
152 62125 0.006197
153 58308 0.005816
154 55277 0.005514
155 52379 0.005225
156 49264 0.004914
157 47111 0.004699
158 44685 0.004457
159 42725 0.004262
160 40908 0.004081
161 � 38969 0.003887
162 � 37297 0.003720
163 � 35654 0.003557
164 � 34353 0.003427
165 � 33394 0.003331
166 � 31932 0.003185
167 � 30974 0.003090
168 � 29621 0.002955
169 � 28867 0.002880
170 � 27737 0.002767
171 � 26791 0.002672
172 � 25657 0.002559
173 � 25178 0.002512
174 � 24418 0.002436
175 � 23560 0.002350
176 � 22887 0.002283
177 � 21884 0.002183
178 � 21656 0.002160
179 � 21169 0.002112
180 � 20386 0.002034
181 � 19882 0.001983
182 � 19530 0.001948
183 � 18937 0.001889
184 � 18366 0.001832
185 � 18042 0.001800
186 � 17285 0.001724
187 � 16930 0.001689
188 � 16679 0.001664
189 � 16303 0.001626
190 � 15903 0.001586
191 � 15609 0.001557
192 � 15178 0.001514
193 � 14822 0.001479
194 � 14550 0.001451
195 � 14178 0.001414
196 � 13897 0.001386
197 � 13673 0.001364
198 � 13357 0.001332
199 � 13353 0.001332
200 � 13086 0.001305
201 � 12794 0.001276
202 � 12378 0.001235
203 � 12359 0.001233
204 � 11972 0.001194
205 � 11917 0.001189
206 � 11434 0.001141
207 � 11601 0.001157
208 � 11397 0.001137
209 � 10922 0.001089
210 � 10849 0.001082
211 � 10891 0.001086
212 � 10564 0.001054
213 � 10638 0.001061
214 � 10143 0.001012
215 � 9993 0.000997
216 � 9855 0.000983
217 � 9736 0.000971
218 � 9632 0.000961
219 � 9492 0.000947
220 � 9424 0.000940
221 � 9494 0.000947
222 � 9416 0.000939
223 � 9114 0.000909
224 � 9120 0.000910
225 � 8793 0.000877
226 � 8703 0.000868
227 � 8664 0.000864
228 � 8631 0.000861
229 � 8625 0.000860
230 � 8542 0.000852
231 � 8490 0.000847
232 � 8397 0.000838
233 � 8352 0.000833
234 � 8246 0.000823
235 � 8186 0.000817
236 � 8092 0.000807
237 � 8063 0.000804
238 � 8037 0.000802
239 � 8017 0.000800
240 � 7923 0.000790
241 � 7944 0.000792
242 � 7862 0.000784
243 � 7808 0.000779
244 � 7770 0.000775
245 � 7565 0.000755
246 � 7822 0.000780
247 � 7711 0.000769
248 � 7761 0.000774
249 � 7814 0.000779
250 � 7674 0.000765
251 � 7644 0.000762
252 � 7598 0.000758
253 � 7665 0.000765
254 � 7616 0.000760
255 � 7484 0.000747
Total: 10025000 1.000000
Entropy = 7.125868 bits per byte.
Optimum compression would reduce the size
of this 10025000 byte file by 10 percent.
Chi square distribution for 10025000 samples is 16920202.99, and randomly
would exceed this value less than 0.01 percent of the times.
Arithmetic mean value of data bytes is 127.8980 (127.5 = random).
Monte Carlo value for Pi is 3.767184392 (error 19.91 percent).
Serial correlation coefficient is 0.000042 (totally uncorrelated = 0.0).Which gives $Pr(X=128) = 0.020433$ and hence $H_{\infty} = -\log_2(0.020433) = 5.613$ bits/byte. That is only 79% of ent’s default measure. A wackier sample distribution with a smaller kurtosis (platykurtic) might drop that percentage considerably lower still. And wacky distributions are certainly possible as you can see elsewhere on this site.
Be ware!
Notes:-
- Also on the
entpage (bottom) is this:-
BUGS: Note that the “optimal compression” shown for the file is computed from the byte- or bit-stream entropy and thus reflects compressibility based on a reading frame of the chosen width (8-bit bytes or individual bits if the -b option is specified). Algorithms which use a larger reading frame, such as the Lempel-Ziv [Lempel & Ziv] algorithm, may achieve greater compression if the file contains repeated sequences of multiple bytes.
-
A consequence of note 1 above is that an 8-bit window presupposes IID data with a relaxation period $\ngtr$ 8 bits. Sadly it is common to see
entused (incorrectly) against non-IID data sets. In those cases the default reported entropy would be much higher than the true rate. -
More about measuring entropy.
-
For interest, $\frac{H_{\infty}}{H_{Compression|ent}} = \frac{5.613}{7.125868} = 0.788 $ for this particular IID Gaussian distribution.