3. Extract
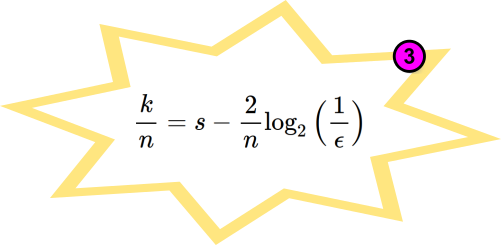
For any TRNG to be worthy of the name, it must satisfy the most important aspect of TRNG design, namely that entropy generated > length output:-
$$ \text{Device} = \left \{ \begin{array}{ccc} \text{TRNG} & \text{if} & H_{in} > H_{out} \\ \text{PRNG} & \text{if} & H_{in} < H_{out} \\ \end{array} \right. $$
which illustrates the humongous danger of using whitening algorithms in TRNGs. With a bit of AES fudging, any entropy source can produce output entropy at almost infinite rates. For instance, the Intel on-chip TRNG (RDRAND) allegedly produces nearly 2 Gb/s. Clearly Rubbish & balderdash.
Thus more formally:-
$$ H_{out} \ngtr H_{in} $$
So post extraction, a weakly random source emerges with much better randomness, and a bias away from perfection bounded by the Leftover Hash Lemma:-
$$ \epsilon = 2^{-(sn-k)/2} $$
where we have $n$ = input bits at $s$ bits/bit of raw entropy from the source, $k$ is the number of output bits from the extractor (and ideally $\ll sn$). $\epsilon$ is the bias away from a perfectly uniform $k$ bit length string, i.e. $H(k) = 1 - \epsilon$ bits/bit. NIST accepts that $\epsilon < 2^{-64}$ for cryptographic applications. But $\epsilon$ can easily be made much smaller. The value $\epsilon$ can therefore be seen as a measure for the quality of the random bits output by the extractor. We recommend a world beating $\epsilon = 2^{-128}$ in conjunction with SHA-512.
Rearranging the above bias equation, we arrive at:-
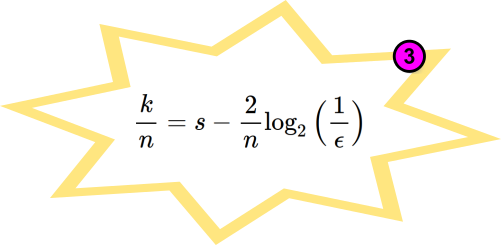
Using the third golden formula, the following charts show the relative input length for a bias of your choosing (remember $2^{-128}$), and the efficiencies. By efficiency, we mean the degree of entropy preservation across the randomness extractor algorithm. Notice for example, that you can achieve >65% efficiency if you use SHA-512 ($k=512$) with an input ($n$) of 768 bits worth of entropy if $s=1$ bit/bit.
We have considered SHA-512, SHA-256, MD5/AES and CRC32 extraction algorithms. CRC32 might sound weird, but it’s used in some retail USB TRNGs as a whitening algorithm. We have not included von Neumann extraction as we are unaware of any literature that provides a direct linkage between the input entropy/autocorrelation and final output bias, $\epsilon$.
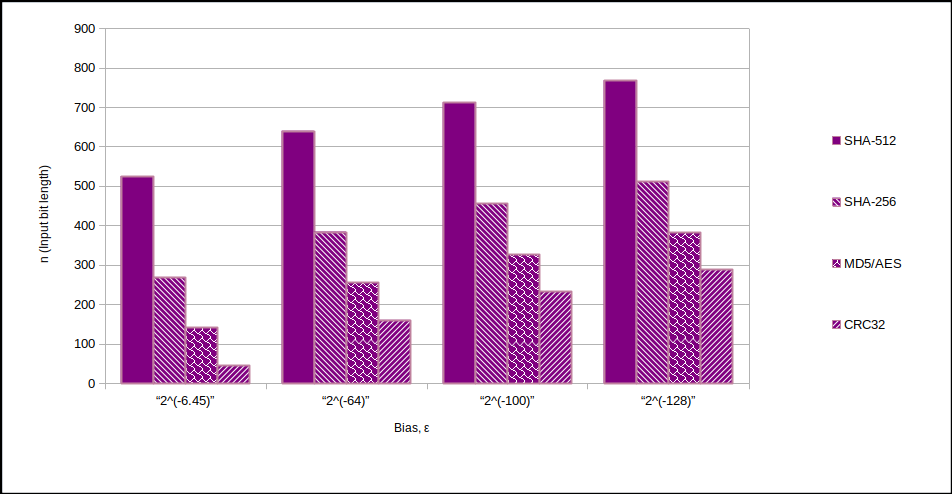
Relationship between output bias ($ \epsilon$) and input length ($n$) post randomness extraction.
And the above input sizes ($n$) in tabular form:-
| $ \epsilon$ | $ \epsilon$ (decimal) | SHA-512 | SHA-256 | MD5/AES | CRC32 |
|---|---|---|---|---|---|
| $2^{-6.45}$ | $0.0114$ | 525 | 269 | 141 | 45 |
| $2^{-64}$ | $5.42 \times10^{-20}$ | 640 | 384 | 256* | 160 |
| $2^{-100}$ | $7.89 \times10^{-31}$ | 712 | 456 | 328 | 232 |
| $2^{-128}$ | $2.94 \times10^{-39}$ | 768 | 512 | 384 | 288 |
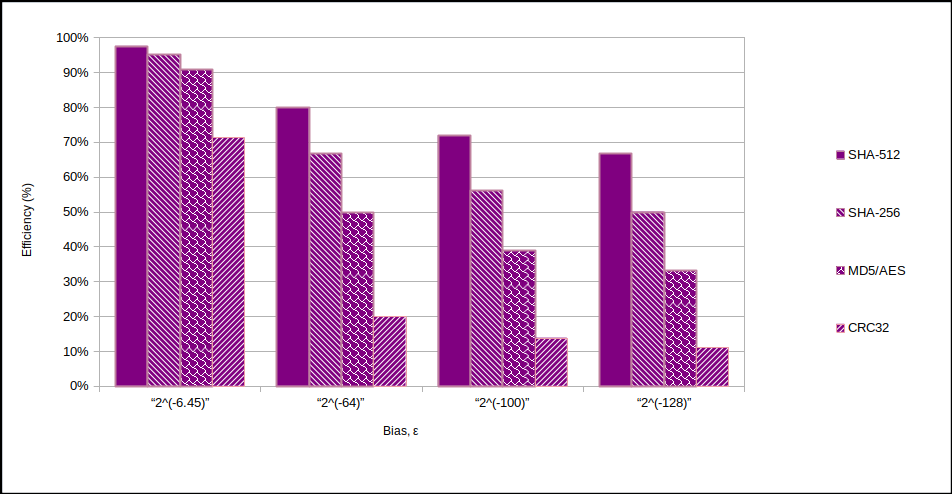
Relationship between output bias ($ \epsilon$) and extractor algorithm efficiency.
The take away is that the wider the block size, the more efficient is the extractor. Therefore always aim to use SHA-512 if extracting on a PC.