Entropy Analysis
Here we test a raw 10MB sample, which incidentally is available for download at the bottom of the page…
The following test proves that entropy is being generated at a principally constant rate throughout that sampling process. $ \chi^2 = 1.0 $ for the 10 chart bars being these values randomly (as expected for a principally constant rate).
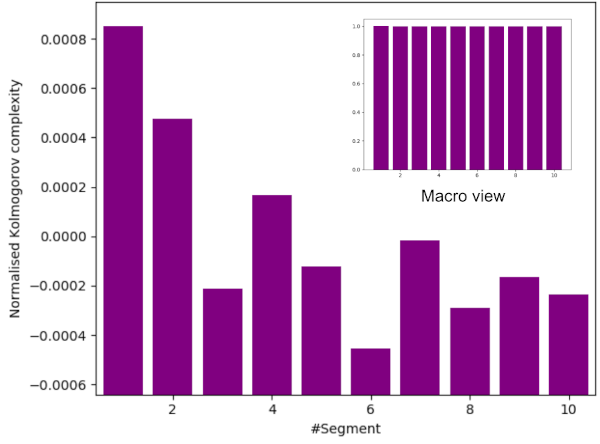
Kolmogorov complexity test for entropy creation.
From ent:- Serial correlation coefficient $(R)$ is 0.000042 which is much less than the commonly accepted value for IID data of $10^{-3}$. Totally uncorrelated = 0.0. As a chart of the autocorrelation up to lag = 100 (ent serial correlation coefficient is only measured for a lag of $n=1$):-
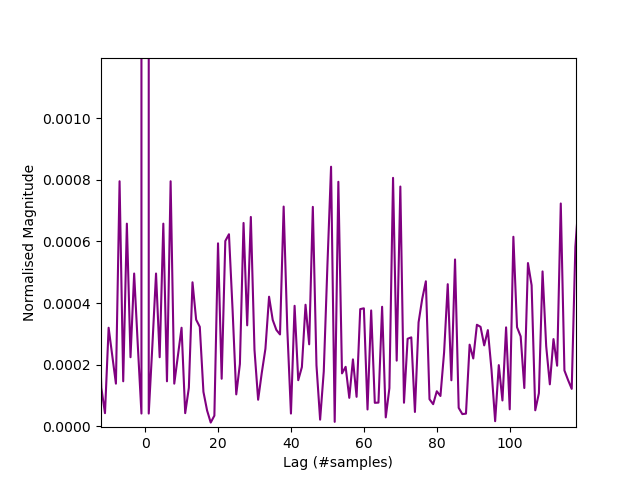
Autocorrelation.
Expand our fast IID test:-
$ python3 iid-test.py /tmp/zener.bin
LZMA tests...
Permutation 1 : NTS = 0.9999603658670847
Permutation 2 : NTS = 1.0000616859655616
Permutation 3 : NTS = 1.0000044088017317
Permutation 4 : NTS = 1.0000352613971446
Permutation 5 : NTS = 0.9999691322638398
Permutation 6 : NTS = 0.999955887283186
Permutation 7 : NTS = 1.0000749426908835
Permutation 8 : NTS = 1.0000396823647162
Permutation 9 : NTS = 0.9999867703868339
Permutation 10 : NTS = 1.0000441018222872
BZ2 tests...
Permutation 1 : NTS = 1.0002786012339844
Permutation 2 : NTS = 0.9997473896056042
Permutation 3 : NTS = 1.0000052227993996
Permutation 4 : NTS = 0.9999644983512617
Permutation 5 : NTS = 1.0000376008171912
Permutation 6 : NTS = 0.9999049220099279
Permutation 7 : NTS = 1.0000229758294275
Permutation 8 : NTS = 1.0001754999921653
Permutation 9 : NTS = 0.9999174835619944
Permutation 10 : NTS = 0.999939414008108
ZLIB tests...
Permutation 1 : NTS = 1.000023271972898
Permutation 2 : NTS = 0.9999689558063729
Permutation 3 : NTS = 0.9999889067859409
Permutation 4 : NTS = 0.9999889091973808
Permutation 5 : NTS = 0.9999534039522324
Permutation 6 : NTS = 0.999892359284733
Permutation 7 : NTS = 1.0000687671709962
Permutation 8 : NTS = 0.9999500797614478
Permutation 9 : NTS = 1.0000099861414549
Permutation 10 : NTS = 0.9999689307633156
-----------------------------------
Broke file into 1,002,500 byte segments.
Tested 10,025,000 bytes for each compressor.
Using 3 compressors.
Minimum NTS = 0.9997473896056042
Maximum NTS = 1.0002786012339844
Mean NTS = 0.9999979805963033
0.0% unchanged by shuffle.
Probability of 14 heads and 16 tails = 0.8555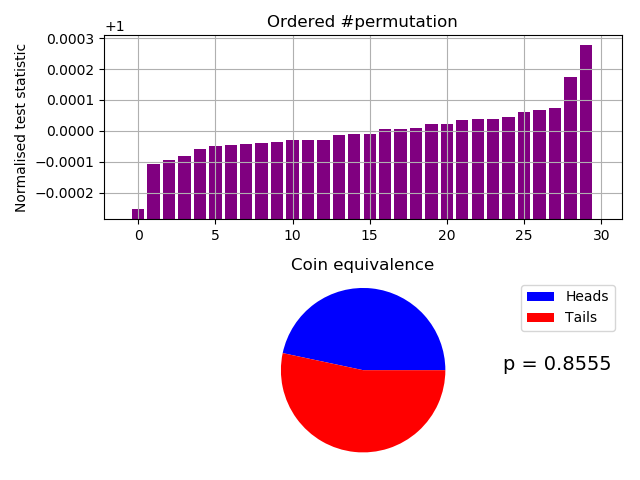
Results of our fast IID test.
Expand our slow IID test:-
run:
Starting IID test...
Baseline: 36730489
Starting a compressor thread...
Starting a compressor thread...
Starting a compressor thread...
Starting a compressor thread...
Starting a compressor thread...
Compressor Thread-3 started.
Compressor Thread-0 started.
Compressor Thread-2 started.
Compressor Thread-4 started.
Compressor Thread-1 started.
Compressor Thread-3 Permutation 1, Normalised statistic = 0.9999902261034423
Compressor Thread-4 Permutation 1, Normalised statistic = 1.0000237132699215
Compressor Thread-1 Permutation 1, Normalised statistic = 1.0000074869681153
Compressor Thread-0 Permutation 1, Normalised statistic = 1.000016362428499
Compressor Thread-2 Permutation 1, Normalised statistic = 0.9999847265850449
CURRENT RANK = 2
Compressor Thread-4 Permutation 2, Normalised statistic = 1.0000048188849324
Compressor Thread-2 Permutation 2, Normalised statistic = 1.0000049822369639
Compressor Thread-0 Permutation 2, Normalised statistic = 1.000013503767946
Compressor Thread-1 Permutation 2, Normalised statistic = 0.9999930303133182
Compressor Thread-3 Permutation 2, Normalised statistic = 1.0000069152360047
CURRENT RANK = 3
Compressor Thread-4 Permutation 3, Normalised statistic = 0.9999892459912526
Compressor Thread-0 Permutation 3, Normalised statistic = 0.9999977947475733
Compressor Thread-1 Permutation 3, Normalised statistic = 0.9999980670009594
Compressor Thread-2 Permutation 3, Normalised statistic = 1.0000054722930587
Compressor Thread-3 Permutation 3, Normalised statistic = 1.0000104817553612
CURRENT RANK = 6
Remaining running time to full completion = 20019s
Estimated full completion date/time = 2021-10-05T08:04:47.189948
Compressor Thread-3 Permutation 4, Normalised statistic = 0.9999840731769185
Compressor Thread-2 Permutation 4, Normalised statistic = 1.0000030492379233
Compressor Thread-0 Permutation 4, Normalised statistic = 1.0000076230948083
Compressor Thread-4 Permutation 4, Normalised statistic = 1.0000132859652373
Compressor Thread-1 Permutation 4, Normalised statistic = 0.9999919957504514
CURRENT RANK = 8
Remaining running time to full completion = 20009s
Estimated full completion date/time = 2021-10-05T08:04:47.189948
Compressor Thread-3 Permutation 5, Normalised statistic = 1.0000030220125846
Compressor Thread-2 Permutation 5, Normalised statistic = 1.0000103456286684
Compressor Thread-0 Permutation 5, Normalised statistic = 1.000020664031998
Compressor Thread-1 Permutation 5, Normalised statistic = 0.9999991015638262
Compressor Thread-4 Permutation 5, Normalised statistic = 0.9999761778287243
CURRENT RANK = 10
Remaining running time to full completion = 19999s
Estimated full completion date/time = 2021-10-05T08:04:47.189948
Compressor Thread-3 Permutation 6, Normalised statistic = 0.9999922680038373
Compressor Thread-2 Permutation 6, Normalised statistic = 1.0000037843220655
Compressor Thread-0 Permutation 6, Normalised statistic = 0.9999762322794015
Compressor Thread-1 Permutation 6, Normalised statistic = 1.000018758258296
Compressor Thread-4 Permutation 6, Normalised statistic = 0.9999910428636003
CURRENT RANK = 13
Remaining running time to full completion = 19989s
Estimated full completion date/time = 2021-10-05T08:04:47.189948
Compressor Thread-3 Permutation 7, Normalised statistic = 1.0000145383308128
Compressor Thread-0 Permutation 7, Normalised statistic = 1.0000212902147858
Compressor Thread-2 Permutation 7, Normalised statistic = 1.0000040838007902
Compressor Thread-1 Permutation 7, Normalised statistic = 0.9999956167204853
Compressor Thread-4 Permutation 7, Normalised statistic = 1.0000267080571674
CURRENT RANK = 14
Remaining running time to full completion = 19979s
Estimated full completion date/time = 2021-10-05T08:04:47.189948
Compressor Thread-3 Permutation 8, Normalised statistic = 1.0000053361663657
Compressor Thread-0 Permutation 8, Normalised statistic = 0.9999930030879796
Compressor Thread-2 Permutation 8, Normalised statistic = 1.0
Compressor Thread-4 Permutation 8, Normalised statistic = 0.9999796898974037
Compressor Thread-1 Permutation 8, Normalised statistic = 0.9999934114680586
CURRENT RANK = 18
Remaining running time to full completion = 19969s
Estimated full completion date/time = 2021-10-05T08:04:47.189948
Compressor Thread-3 Permutation 9, Normalised statistic = 0.9999906344835213
Compressor Thread-0 Permutation 9, Normalised statistic = 1.0000047372089165
Compressor Thread-4 Permutation 9, Normalised statistic = 0.999991614595711
Compressor Thread-2 Permutation 9, Normalised statistic = 0.9999955894951467
Compressor Thread-1 Permutation 9, Normalised statistic = 1.0000032398152936
CURRENT RANK = 21
Remaining running time to full completion = 19959s
Estimated full completion date/time = 2021-10-05T08:04:47.189948
Compressor Thread-3 Permutation 10, Normalised statistic = 0.9999940921015236
Compressor Thread-0 Permutation 10, Normalised statistic = 1.0000048733356095
Compressor Thread-2 Permutation 10, Normalised statistic = 0.999980561108239
Compressor Thread-1 Permutation 10, Normalised statistic = 1.0000053633917043
Compressor Thread-4 Permutation 10, Normalised statistic = 0.9999870407388259
Compressor Thread-3 Permutation 11, Normalised statistic = 1.000009692220542
CURRENT RANK = 24
Remaining running time to full completion = 19555s
Estimated full completion date/time = 2021-10-05T07:58:13.189948
Compressor Thread-0 Permutation 11, Normalised statistic = 1.000012142501016
Compressor Thread-1 Permutation 11, Normalised statistic = 1.0000004900560948
Compressor Thread-4 Permutation 11, Normalised statistic = 0.9999889737378667
Compressor Thread-2 Permutation 11, Normalised statistic = 1.0000350934614566
Compressor Thread-3 Permutation 12, Normalised statistic = 0.9999927308345936
Compressor Thread-0 Permutation 12, Normalised statistic = 0.9999923496798532
Compressor Thread-1 Permutation 12, Normalised statistic = 0.9999913695676635
Compressor Thread-2 Permutation 12, Normalised statistic = 1.0000007078588036
Compressor Thread-4 Permutation 12, Normalised statistic = 1.0000176964700906
CURRENT RANK = 28
Remaining running time to full completion = 18268s
Estimated full completion date/time = 2021-10-05T07:36:56.189948
Compressor Thread-3 Permutation 13, Normalised statistic = 1.0000169069352711
Compressor Thread-0 Permutation 13, Normalised statistic = 1.000012006374323
Compressor Thread-2 Permutation 13, Normalised statistic = 1.0000002450280474
Compressor Thread-1 Permutation 13, Normalised statistic = 1.0000153823163094
Compressor Thread-4 Permutation 13, Normalised statistic = 0.9999892187659141
CURRENT RANK = 29
Remaining running time to full completion = 18386s
Estimated full completion date/time = 2021-10-05T07:39:04.189948
Compressor Thread-3 Permutation 14, Normalised statistic = 1.0000041382514673
Compressor Thread-0 Permutation 14, Normalised statistic = 1.0000082492775961
Compressor Thread-2 Permutation 14, Normalised statistic = 1.0000127959091425
Compressor Thread-1 Permutation 14, Normalised statistic = 1.0000080042495487
Compressor Thread-4 Permutation 14, Normalised statistic = 1.0000016879709932
CURRENT RANK = 29
Remaining running time to full completion = 18486s
Estimated full completion date/time = 2021-10-05T07:40:54.189948
Compressor Thread-3 Permutation 15, Normalised statistic = 1.0000062618278782
Compressor Thread-0 Permutation 15, Normalised statistic = 0.9999967057340293
Compressor Thread-2 Permutation 15, Normalised statistic = 0.9999964879313205
Compressor Thread-1 Permutation 15, Normalised statistic = 1.0000113801915351
Compressor Thread-4 Permutation 15, Normalised statistic = 1.000008603206998
CURRENT RANK = 31
Remaining running time to full completion = 18572s
Estimated full completion date/time = 2021-10-05T07:42:30.189948
Compressor Thread-3 Permutation 16, Normalised statistic = 1.0000001089013544
Compressor Thread-0 Permutation 16, Normalised statistic = 1.0000047372089165
Compressor Thread-2 Permutation 16, Normalised statistic = 0.9999936292707674
Compressor Thread-1 Permutation 16, Normalised statistic = 0.999980833361625
Compressor Thread-4 Permutation 16, Normalised statistic = 0.999998366479684
CURRENT RANK = 34
Remaining running time to full completion = 18645s
Estimated full completion date/time = 2021-10-05T07:43:53.189948
Compressor Thread-3 Permutation 17, Normalised statistic = 0.9999887287098193
Compressor Thread-0 Permutation 17, Normalised statistic = 1.000012333078386
Compressor Thread-1 Permutation 17, Normalised statistic = 1.0000082492775961
Compressor Thread-4 Permutation 17, Normalised statistic = 1.000010645107393
Compressor Thread-2 Permutation 17, Normalised statistic = 1.0000121152756773
CURRENT RANK = 35
Remaining running time to full completion = 18709s
Estimated full completion date/time = 2021-10-05T07:45:07.189948
Compressor Thread-3 Permutation 18, Normalised statistic = 0.9999837192475167
Compressor Thread-0 Permutation 18, Normalised statistic = 0.9999958617485327
Compressor Thread-1 Permutation 18, Normalised statistic = 1.000002178027088
Compressor Thread-2 Permutation 18, Normalised statistic = 0.9999897360473475
Compressor Thread-4 Permutation 18, Normalised statistic = 1.0000011979148984
CURRENT RANK = 38
Remaining running time to full completion = 18765s
Estimated full completion date/time = 2021-10-05T07:46:13.189948
Compressor Thread-3 Permutation 19, Normalised statistic = 1.0000084398549662
Compressor Thread-0 Permutation 19, Normalised statistic = 1.0000011979148984
Compressor Thread-1 Permutation 19, Normalised statistic = 1.000005118363657
Compressor Thread-4 Permutation 19, Normalised statistic = 1.0000022052524267
Compressor Thread-2 Permutation 19, Normalised statistic = 0.9999908522862301
Compressor Thread-3 Permutation 20CURRENT RANK = 40
, Normalised statistic = 0.999974081477652
Remaining running time to full completion = 18615s
Estimated full completion date/time = 2021-10-05T07:43:53.189948
Compressor Thread-0 Permutation 20, Normalised statistic = 1.0000050366876412
Compressor Thread-1 Permutation 20, Normalised statistic = 1.000009964473928
Compressor Thread-2 Permutation 20, Normalised statistic = 0.9999970596634311
Compressor Thread-4 Permutation 20, Normalised statistic = 0.9999906344835213
Compressor Thread-3 Permutation 21, Normalised statistic = 1.0000125236557564
Compressor Thread-0 Permutation 21, Normalised statistic = 0.9999992104651806
CURRENT RANK = 43
Remaining running time to full completion = 18483s
Estimated full completion date/time = 2021-10-05T07:41:51.189948
Compressor Thread-1 Permutation 21, Normalised statistic = 0.9999898449487019
Compressor Thread-4 Permutation 21, Normalised statistic = 1.0000002994787247
Compressor Thread-2 Permutation 21, Normalised statistic = 1.0000084126296276
Compressor Thread-3 Permutation 22, Normalised statistic = 1.0000004356054175
Compressor Thread-0 Permutation 22, Normalised statistic = 1.0000054450677203
Compressor Thread-1 Permutation 22, Normalised statistic = 1.0000028586605532
Compressor Thread-4 Permutation 22, Normalised statistic = 1.000002178027088
Compressor Thread-2 Permutation 22, Normalised statistic = 0.9999990198878104
CURRENT RANK = 45
Remaining running time to full completion = 18026s
Estimated full completion date/time = 2021-10-05T07:34:24.189948
Compressor Thread-3 Permutation 23, Normalised statistic = 0.9999726657600447
Compressor Thread-0 Permutation 23, Normalised statistic = 0.9999898993993791
Compressor Thread-1 Permutation 23, Normalised statistic = 1.000010100600621
Compressor Thread-2 Permutation 23, Normalised statistic = 0.9999954533684536
Compressor Thread-4 Permutation 23, Normalised statistic = 1.0000187854836347
CURRENT RANK = 48
Remaining running time to full completion = 18095s
Estimated full completion date/time = 2021-10-05T07:35:43.189948
Compressor Thread-3 Permutation 24, Normalised statistic = 0.9999853527678327
Compressor Thread-0 Permutation 24, Normalised statistic = 0.9999991560145034
Compressor Thread-1 Permutation 24, Normalised statistic = 0.9999861423026521
Compressor Thread-2 Permutation 24, Normalised statistic = 1.000008793784368
Compressor Thread-4 Permutation 24, Normalised statistic = 0.99999338424272
CURRENT RANK = 52
Remaining running time to full completion = 18158s
Estimated full completion date/time = 2021-10-05T07:36:56.189948
Compressor Thread-3 Permutation 25, Normalised statistic = 0.999999319366535
Compressor Thread-0 Permutation 25, Normalised statistic = 1.000013503767946
Compressor Thread-1 Permutation 25, Normalised statistic = 0.9999995371692438
Compressor Thread-2 Permutation 25, Normalised statistic = 1.0000039748994358
Compressor Thread-4 Permutation 25, Normalised statistic = 1.000005581194413
CURRENT RANK = 54
Remaining running time to full completion = 18215s
Estimated full completion date/time = 2021-10-05T07:38:03.189948
Compressor Thread-3 Permutation 26, Normalised statistic = 0.9999931936653498
Compressor Thread-0 Permutation 26, Normalised statistic = 1.000010971811456
Compressor Thread-1 Permutation 26, Normalised statistic = 1.000017396991366
Compressor Thread-4 Permutation 26, Normalised statistic = 1.0000179959488151
Compressor Thread-2 Permutation 26, Normalised statistic = 0.9999838553742096
CURRENT RANK = 56
Remaining running time to full completion = 18266s
Estimated full completion date/time = 2021-10-05T07:39:04.189948
Compressor Thread-3 Permutation 27, Normalised statistic = 1.00001848600491
Compressor Thread-0 Permutation 27, Normalised statistic = 0.9999969779874153
Compressor Thread-1 Permutation 27, Normalised statistic = 0.999997821972912
Compressor Thread-4 Permutation 27, Normalised statistic = 1.0000184043288942
Compressor Thread-2 Permutation 27, Normalised statistic = 0.9999989926624717
CURRENT RANK = 59
Remaining running time to full completion = 18313s
Estimated full completion date/time = 2021-10-05T07:40:01.189948
Compressor Thread-3 Permutation 28, Normalised statistic = 1.0000118157969529
Compressor Thread-0 Permutation 28, Normalised statistic = 1.0000036754207111
Compressor Thread-1 Permutation 28, Normalised statistic = 1.0000039476740972
Compressor Thread-4 Permutation 28, Normalised statistic = 0.9999852710918169
Compressor Thread-2 Permutation 28, Normalised statistic = 1.0000115979942439
CURRENT RANK = 60
Remaining running time to full completion = 18356s
Estimated full completion date/time = 2021-10-05T07:40:54.189948
Compressor Thread-3 Permutation 29, Normalised statistic = 0.9999894910193001
Compressor Thread-0 Permutation 29, Normalised statistic = 1.0000091477137698
Compressor Thread-4 Permutation 29, Normalised statistic = 0.9999995371692438
Compressor Thread-2 Permutation 29, Normalised statistic = 1.0000110262621333
Compressor Thread-1 Permutation 29, Normalised statistic = 0.9999933297920428
Compressor Thread-3 Permutation 30, Normalised statistic = 0.9999768584621893
CURRENT RANK = 64
Remaining running time to full completion = 18268s
Estimated full completion date/time = 2021-10-05T07:39:36.189948
Compressor Thread-4 Permutation 30, Normalised statistic = 1.0000049277862868
Compressor Thread-0 Permutation 30, Normalised statistic = 1.0000052272650113
Compressor Thread-2 Permutation 30, Normalised statistic = 0.9999983937050225
Compressor Thread-1 Permutation 30, Normalised statistic = 1.0000036209700338
Compressor Thread-3 Permutation 31, Normalised statistic = 1.0000034576180024
Compressor Thread-4 Permutation 31, Normalised statistic = 0.999985134965124
Compressor Thread-2 Permutation 31, Normalised statistic = 1.0000117885716142
Compressor Thread-0 Permutation 31, Normalised statistic = 1.0000071874893905
Compressor Thread-1 Permutation 31, Normalised statistic = 1.000013503767946
CURRENT RANK = 66
Remaining running time to full completion = 17828s
Estimated full completion date/time = 2021-10-05T07:32:26.189948
Compressor Thread-3 Permutation 32, Normalised statistic = 1.0000039204487585
Compressor Thread-4 Permutation 32, Normalised statistic = 1.0000123875290634
Compressor Thread-0 Permutation 32, Normalised statistic = 1.0000232776645037
Compressor Thread-2 Permutation 32, Normalised statistic = 1.000014048274718
Compressor Thread-1 Permutation 32, Normalised statistic = 0.9999964879313205
CURRENT RANK = 67
Remaining running time to full completion = 17879s
Estimated full completion date/time = 2021-10-05T07:33:27.189948
Compressor Thread-3 Permutation 33, Normalised statistic = 0.9999765589834647
Compressor Thread-4 Permutation 33, Normalised statistic = 0.9999872313161962
Compressor Thread-0 Permutation 33, Normalised statistic = 1.0000067791093117
Compressor Thread-2 Permutation 33, Normalised statistic = 1.0000161446257902
Compressor Thread-1 Permutation 33, Normalised statistic = 1.0000142933027654
CURRENT RANK = 69
Remaining running time to full completion = 17926s
Estimated full completion date/time = 2021-10-05T07:34:24.189948
Compressor Thread-3 Permutation 34, Normalised statistic = 0.9999938470734762
Compressor Thread-4 Permutation 34, Normalised statistic = 1.0000015246189617
Compressor Thread-1 Permutation 34, Normalised statistic = 1.0000092293897858
Compressor Thread-0 Permutation 34, Normalised statistic = 1.0000030492379233
Compressor Thread-2 Permutation 34, Normalised statistic = 0.9999893821179456
CURRENT RANK = 71
Remaining running time to full completion = 17969s
Estimated full completion date/time = 2021-10-05T07:35:17.189948
Compressor Thread-3 Permutation 35, Normalised statistic = 0.9999978764235892
Compressor Thread-4 Permutation 35, Normalised statistic = 1.0000031581392776
Compressor Thread-1 Permutation 35, Normalised statistic = 0.9999991560145034
Compressor Thread-0 Permutation 35, Normalised statistic = 1.0000039204487585
Compressor Thread-2 Permutation 35, Normalised statistic = 0.9999899810753949
CURRENT RANK = 74
Remaining running time to full completion = 18010s
Estimated full completion date/time = 2021-10-05T07:36:08.189948
Compressor Thread-3 Permutation 36, Normalised statistic = 1.0000003267040631
Compressor Thread-4 Permutation 36, Normalised statistic = 1.0000118430222913
Compressor Thread-0 Permutation 36, Normalised statistic = 0.9999984209303612
Compressor Thread-2 Permutation 36, Normalised statistic = 0.999987312992212
Compressor Thread-1 Permutation 36, Normalised statistic = 1.000001905773702
CURRENT RANK = 76
Remaining running time to full completion = 18048s
Estimated full completion date/time = 2021-10-05T07:36:56.189948
Compressor Thread-3 Permutation 37, Normalised statistic = 0.9999932753413656
Compressor Thread-4 Permutation 37, Normalised statistic = 1.0000156273443568
Compressor Thread-0 Permutation 37, Normalised statistic = 1.000008603206998
Compressor Thread-2 Permutation 37, Normalised statistic = 1.000019575018454
Compressor Thread-1 Permutation 37, Normalised statistic = 1.0000071058133748
Compressor Thread-3 Permutation 38, Normalised statistic = 0.9999966512833521
CURRENT RANK = 78
Remaining running time to full completion = 17984s
Estimated full completion date/time = 2021-10-05T07:36:02.189948
Compressor Thread-4 Permutation 38, Normalised statistic = 1.0000096649952033
Compressor Thread-0 Permutation 38, Normalised statistic = 1.000011107938149
Compressor Thread-2 Permutation 38, Normalised statistic = 1.000007568644131
Compressor Thread-1 Permutation 38, Normalised statistic = 1.0000088482350453
Compressor Thread-3 Permutation 39, Normalised statistic = 1.0000030492379233
Compressor Thread-0 Permutation 39, Normalised statistic = 0.9999983937050225
Compressor Thread-1 Permutation 39, Normalised statistic = 1.000009746671219
Compressor Thread-4 Permutation 39, Normalised statistic = 0.9999953444670993
CURRENT RANK = 80
Remaining running time to full completion = 17735s
Estimated full completion date/time = 2021-10-05T07:32:03.189948
Compressor Thread-2 Permutation 39, Normalised statistic = 0.9999791998413089
Compressor Thread-3 Permutation 40, Normalised statistic = 1.0000030220125846
Compressor Thread-1 Permutation 40, Normalised statistic = 0.9999912334409705
Compressor Thread-4 Permutation 40, Normalised statistic = 1.000000680633465
Compressor Thread-2 Permutation 40, Normalised statistic = 1.0000108901354403
Compressor Thread-0 Permutation 40, Normalised statistic = 0.9999830386140517
CURRENT RANK = 83
Remaining running time to full completion = 17684s
Estimated full completion date/time = 2021-10-05T07:31:22.189948
Compressor Thread-3 Permutation 41, Normalised statistic = 1.0000144838801357
Compressor Thread-1 Permutation 41, Normalised statistic = 1.0000060712505079
Compressor Thread-4 Permutation 41, Normalised statistic = 1.0000117885716142
Compressor Thread-0 Permutation 41, Normalised statistic = 0.9999922407784988
Compressor Thread-2 Permutation 41, Normalised statistic = 1.0000047916595938
CURRENT RANK = 84
Remaining running time to full completion = 17722s
Estimated full completion date/time = 2021-10-05T07:32:10.189948
Compressor Thread-3 Permutation 42, Normalised statistic = 1.0000007350841422
Compressor Thread-1 Permutation 42, Normalised statistic = 0.9999948271856658
Compressor Thread-0 Permutation 42, Normalised statistic = 1.0000126053317722
Compressor Thread-4 Permutation 42, Normalised statistic = 1.000003348716648
Compressor Thread-2 Permutation 42, Normalised statistic = 1.0000107267834086
CURRENT RANK = 85
Remaining running time to full completion = 17759s
Estimated full completion date/time = 2021-10-05T07:32:57.189948
Compressor Thread-3 Permutation 43, Normalised statistic = 0.999999047113149
Compressor Thread-1 Permutation 43, Normalised statistic = 0.9999760689273699
Compressor Thread-0 Permutation 43, Normalised statistic = 0.9999910428636003
Compressor Thread-2 Permutation 43, Normalised statistic = 0.9999942554535552
Compressor Thread-4 Permutation 43, Normalised statistic = 0.999975306617889
CURRENT RANK = 90
Remaining running time to full completion = 17793s
Estimated full completion date/time = 2021-10-05T07:33:41.189948
Compressor Thread-3 Permutation 44, Normalised statistic = 0.999987721372291
Compressor Thread-1 Permutation 44, Normalised statistic = 0.9999968146353837
Compressor Thread-2 Permutation 44, Normalised statistic = 1.0000367814324498
Compressor Thread-0 Permutation 44, Normalised statistic = 0.9999847538103835
Compressor Thread-4 Permutation 44, Normalised statistic = 0.9999683369312072
CURRENT RANK = 94
Remaining running time to full completion = 17826s
Estimated full completion date/time = 2021-10-05T07:34:24.189948
Compressor Thread-3 Permutation 45, Normalised statistic = 0.9999972230154627
Compressor Thread-1 Permutation 45, Normalised statistic = 1.0000176147940747
Compressor Thread-2 Permutation 45, Normalised statistic = 0.9999998094226298
Compressor Thread-4 Permutation 45, Normalised statistic = 0.9999979580996049
Compressor Thread-0 Permutation 45, Normalised statistic = 0.9999970868887698
Compressor Thread-3 Permutation 46, Normalised statistic = 0.9999982031276523
CURRENT RANK = 99
Remaining running time to full completion = 17775s
Estimated full completion date/time = 2021-10-05T07:33:43.189948
Compressor Thread-1 Permutation 46, Normalised statistic = 1.000002259703104
Compressor Thread-2 Permutation 46, Normalised statistic = 1.0000046827582394
Compressor Thread-0 Permutation 46, Normalised statistic = 0.9999981214516366
Compressor Thread-4 Permutation 46, Normalised statistic = 1.0000086304323366
Compressor Thread-3 Permutation 47, Normalised statistic = 1.0000049550116255
CURRENT RANK = 100
Remaining running time to full completion = 17806s
Estimated full completion date/time = 2021-10-05T07:34:24.189948
----------------------------------
Ranked as > 100/10,000
*** PASSED permutation test. There is no evidence that the data is not IID ***
Based on 231 permutations.
Test results in file: /tmp/results.json
----------------------------------
Compressor Thread-1 Permutation 47, Normalised statistic = 0.9999970596634311
Compressor Thread-2 Permutation 47, Normalised statistic = 1.0000071330387135
Compressor Thread-4 Permutation 47, Normalised statistic = 1.0000048461102709
Compressor Thread-0 Permutation 47, Normalised statistic = 0.9999936020454288
Compressor Thread-3 Permutation 48, Normalised statistic = 1.0000024775058127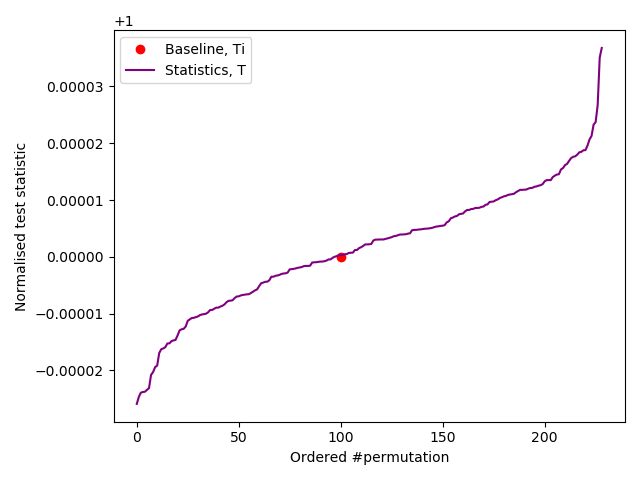
Results of our slow IID test.
Expand NIST’s IID test:-
Opening file: '/tmp/zener.bin'
Loaded 10025000 samples of 256 distinct 8-bit-wide symbols
Number of Binary samples: 80200000
Calculating baseline statistics...
Raw Mean: 127.898049
Median: 128.000000
Binary: false
Literal MCV Estimate: mode = 204840, p-hat = 0.020432917705735659, p_u = 0.020548012901193548
Bitstring MCV Estimate: mode = 40186760, p-hat = 0.50108179551122189, p_u = 0.50122560875628075
H_original: 5.604857
H_bitstring: 0.996468
min(H_original, 8 X H_bitstring): 5.604857 <=======
Chi square independence
score = 60428.242311
degrees of freedom = 60202
p-value = 0.256841
Chi square goodness of fit
score = 2333.011741
degrees of freedom = 2295
p-value = 0.285078
** Passed chi square tests
LiteralLongest Repeated Substring results
P_col: 0.0104992
Length of LRS: 7
Pr(X >= 1): 0.506733
** Passed length of longest repeated substring test
Beginning initial tests...
Initial test results
excursion: 73206.9
numDirectionalRuns: 6.68088e+06
lenDirectionalRuns: 10
numIncreasesDecreases: 5.06483e+06
numRunsMedian: 5.00957e+06
lenRunsMedian: 24
avgCollision: 12.1989
maxCollision: 52
periodicity(1): 105126
periodicity(2): 105029
periodicity(8): 104718
periodicity(16): 105837
periodicity(32): 104999
covariance(1): 1.63989e+11
covariance(2): 1.63984e+11
covariance(8): 1.63986e+11
covariance(16): 1.6399e+11
covariance(32): 1.6399e+11
compression: 9.83242e+06
Beginning permutation tests... these may take some time
83.62% of Permutuation test rounds, 100.00% of Permutuation tests
statistic C[i][0] C[i][1] C[i][2]
----------------------------------------------------
excursion 67 0 6
numDirectionalRuns 28 0 6
lenDirectionalRuns 1 5 5
numIncreasesDecreases 6 0 8
numRunsMedian 7 0 6
lenRunsMedian 7 1 5
avgCollision 6 0 32
maxCollision 3 3 10
periodicity(1) 7 0 6
periodicity(2) 21 0 6
periodicity(8) 153 0 6
periodicity(16) 6 0 118
periodicity(32) 8 0 6
covariance(1) 6 0 6
covariance(2) 36 0 6
covariance(8) 6 0 7
covariance(16) 6 0 12
covariance(32) 6 0 9
compression 6 0 25
(* denotes failed test)
** Passed IID permutation testsTherefore on the basis that all of the above tests were passed with flying colours (but mainly purple), we can confidently conclude that the Zenerglass output is very much IID. So in accordance with our Golden Rule #2 and it’s corresponding Golden Equation #2, $H_{\infty} = - \log_2(p_{max})$ taken at 27.4°C internal temperature:-
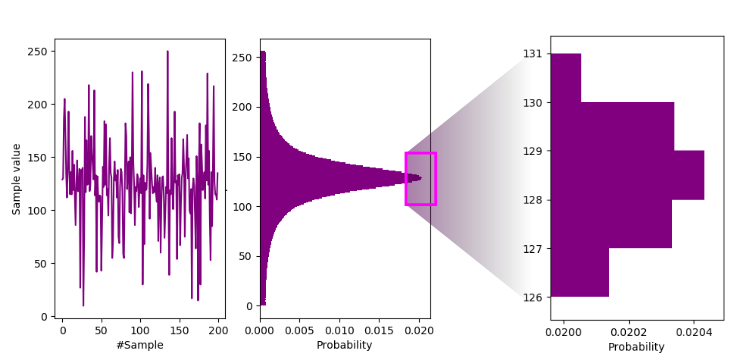
Sample waveform and histogram.
So $H_{\infty} \approx - \log_2(0.0204) = 5.6$. Or, simply and more accurately(!) read it from the NIST IID test: $H_{\infty} = 5.604857$ bits/byte.
Let’s call that 5.5 bits/byte.
- raw-zenerglass.zip (8 MB)